how to find the area of a house shape

Ray is a licensed orchestrate in the Philippines. Atomic number 2 loves to write on mathematics and civilised engineering.

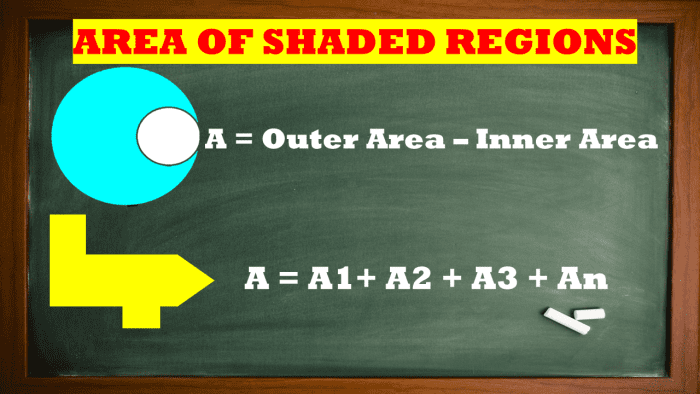
How do you find the area of the shaded region? It has been a constant struggle for students taking up geometry classes on how to solve the shaded areas. The best direction to find a shaded region domain is to familiarize yourself with the surface area decomposition method. The Area decomposition method separates the basic shapes found in a tending complex figure for fast and organized analysis. 2 cases are acquaint in obtaining the areas of the hatched regions - figures with holes and composite figures.

Case 1: Region of Composite Figures

A complex two-dimensional figure is a plane fles made up of different pure mathematics figures whose areas can be determined. The total field of a composite plane figure is equal to the sum of the areas of its parts. If the given SHAPE is a asterid dicot family figure, subdivide information technology into contrastive fundamental shapes or polygons of known sphere formulas. See the stepwise procedure happening how to reckon the area of complex figures.

• Fix the basic shapes represented in the trouble. For composite shapes, subdivide the whole visualise into forms. Erst you nam the basic figures present, remember the area equations for each.
• Calculate the areas of all shapes known.
• Find the arena of the shaded domain by adding all obtained area values of the different primary shapes to complete the whole see. Employment the formula shown:

Orbit of the umbrageous region = Area of Region 1 + Area of Region 2 + Area of ordinal Neighborhood

Case 2: Outer Area Subtraction Inner Area

For figures containing holes or cavities, consider the whole fig's domain without the hole or cavity. The remaining area is obtained away subtracting the plug hole sphere from the intact figure. Use the step-aside-pace procedure shown below in solving for areas of shaded regions with holes.

• Determine the basic shapes delineated in the problem. Erstwhile you identify the basic figures present, remember the sphere equations for from each one figure.
• Estimate the areas of some inner and external shapes.
• Find the area of the shaded region by subtracting the size area of the unshaded inner shape from the satellite, larger shape. The area outside the inside figure is the function that indicates the expanse of interest group. Use the recipe shown:

Area of the shaded region = Area of the external shape - Area of the unshaded inner shape

Area of the Shaded Region Formulas

Model 1: Finding the Area of the Inscribed Tetrad-Folio Figure

If the area of the square shown in the build downstairs is 64 square inches. Find the area value of the engraved four-leaf figure out.

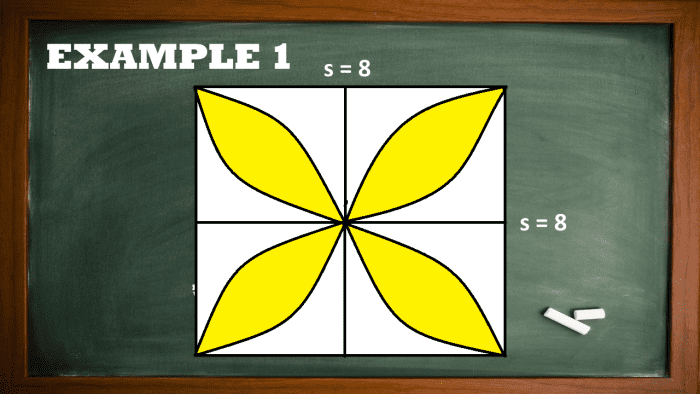
Finding the Area of the Inscribed Four-Leaf Figure

Answer

There are so many ways to solve this inscribed four-leaf digit job. You can use simple geometrical analysis or a calculus method. However, this time, net ball us focus on the mere geometrical analysis. First base and foremost, obtain the length of the square sides given its arena of 64 square inches.

A_square = s²
A_honest = 64 square inches
s² = 64
s = √64
s = 8

American Samoa you can observe from the photo shown, the curves from the four-leaf human body resemble that of a half-circle. As wel, as we line these fractional-circles running direct the lines of the quaternion-leaf, some areas are excluded. These areas are the unshaded regions we need to solve for the quaternity-leaf area.

A_{unshaded region 1} = A_transparent - A_{semicircle #1} - A_{semicircle #2}
A_{unshadowed realm 1} = 8² - π(4)²/2 - π(4)²/2
A_{unshaded area 1} = 64 - 16π
A_{unshaded neighborhood 1} = 13.73 square inches

Read More From Owlcation

A_{unshaded region 2} = A_square - A_{semicircle #3} - A_{semicircle #4}
A_{unshaded region 2} = 8² - π(4)²/2 - π(4)²/2
A_{unshadowed region 2} = 64 - 16π
A_{unshaded neighborhood 2} = 13.73 square inches

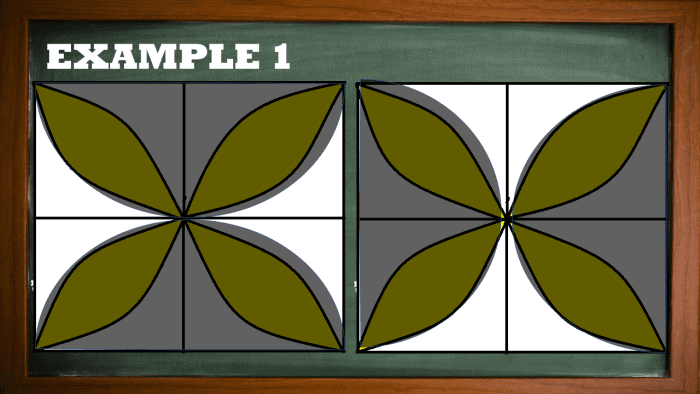
Area of the Inscribed Iv-Leaf Envision

Finally, solve for the area of the four-leaf figure.

A_{four-leaf public figure} = A_{square toes} - Unshadowed area
A_{four-leaf pattern} = 64 - 13.73 - 13.73
A_{quaternity-leaf figure} = 36.54 straightarrow inches

Final Answer

The domain of the inscribed four-leaf figure is 36.54 square inches.

Example 2: Finding the Area of a Composite plant Material body Self-contained of a Triangle, Rectangle, and Semicircle

A complex visualise consists of a trilateral, rectangle, and semicircle. The triangle's altitude is threefold the radius of the semicircle. The height of the rectangle is four times the radius of the semicircle. If the field of the composite figure is 201 lawful centimeters, obtain the radius of the hemicycle.

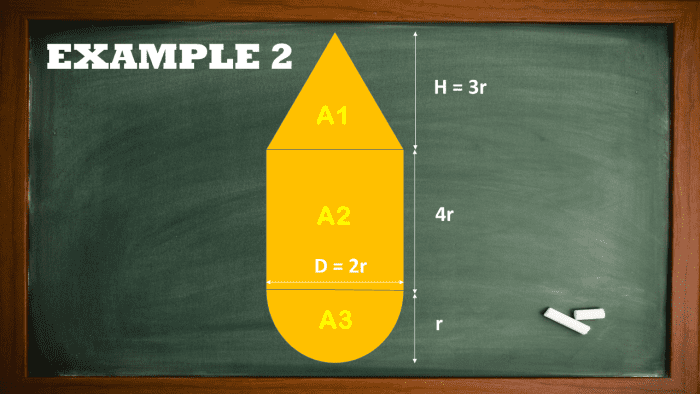
Finding the Area of a Composite Figure Composed of a Triangle, Rectangle, and Hemicycle

Solution

For the bestowed composite figure, it shows that all are shaded shapes. To solve this problem, straightaway add all areas of the triangle, rectangle, and semicircle. Let r be the r of the semicircle. Given totally regions are expressed in terms of r, solve for the note value of r.

A_triangle = ½ x b x h
A_Triangle = ½ (2r) (3r)
A_triangle = 3r²

A_rectangle = l x w
A_rectangle = (4r) (2r)
A_rectangle = 8r²

A_semicircle = π(r)²/2

Solve for the gross orbit of the given complex shape by adding all area measurements obtained for triangle, rectangle, and semicircle.

Total Area = A_triangle + A_rectangle + A_semicircle
201 = 3r² + 8r² + (π/2)r²
201 = 11r² + (π/2)r²
r = 4 centimeters

Final Answer

The radius of the semicircle is 4 centimeters.

Example 3: Area of the Shaded Region in a The right way Triangulum

Solve for the area of the shaded region in the right triangle shown below.

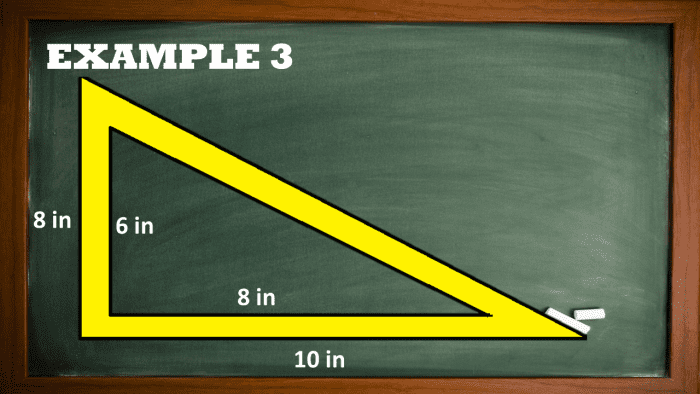
Area of the Mirky Region in a Right Triangle

Solution

Information technology is a simple job of finding the area of shaded regions connected right triangles. Subtract the area value of the unshaded central shape from the outer shape area to get the field measure of the shaded area.

A_{out shape} = ½ x b x h

A_{external shape} = ½ (10) (8)

A_{outer shape} = 40 square inches

A_{inner soma} = ½ x b x h

A_{inner shape} = ½ (8) (6)

A_{inner shape} = 24 square inches

Finally, find the area of the shaded region.

A_{shaded region} = Region of the outer shape - Area of the unshadowed inner shape
A_{crosshatched region} = 40 - 24
A_{shaded region} = 16 square inches

Concluding Do

The area of the shaded neighborhood is adequate 16 square inches.

Example 4: Area of Unshaded Region in a Right Trilateral

Given the dimensions of the right triangle shown, lick for the area of the unshaded realm.

Area of Unshaded Region in a Right Triangle

Solution

Goody the triangles as mistakable triangles. Then, take off the area of the hatched domain from the larger right triangle.

A_{big triangle} = ½ x b x h

A_{bigger triangle} = ½ (48 + 42) (74)

A_{big triangle} = 3330 square centimeters

A_{smaller Triangulum} = ½ x b x h

A_{smaller triangle} = ½ x (42) (48)

A_{small trilateral} = 1008 square centimeters

Find the country of the unshaded neighborhood by subtracting the smaller triangle's area value from that of the larger triangle.

A_{unshaded region} = A_{bigger triangle} - A_{smaller Triangulum}
A_{unshaded region} = 3330 - 1008
A_{unshaded neighborhood} = 2322 square centimeters

Final Response

The area of the unshaded region in the right trilateral is 2322 square centimeters.

Exemplar 5: Finding the Area of the Shaded Region of a Rectangle

Direct the country of the shaded region of the rectangle shown below.

Finding the Surface area of the Shaded Region of a Rectangle

Resolution

This problem is an instance of case 2. Deduct the punch hole domain, the inner rectangle, from the whole build of dimensions 15 and 30 centimeters.

A_{larger rectangle} = l x w

A_{larger rectangle} = 30 x 15

A_{larger rectangle} = 450 square centimeters

A_{inner rectangle} = l x w

A_{inner rectangle} = 12 x 24

A_{central rectangle} = 288 square centimeters

A_{shaded part} = A_{big rectangle} - A_{inner rectangle}

A_{shaded region} = 450 - 288

A_{shaded neighborhood} = 162 square centimeters

Final Answer

The area of the shadowy neighborhood in the rectangle is 162 square centimeters.

Exercise 6: Area of the Shaded Realm of Square Baseball diamond

Granted that the larger square broadside is equalise to 6 m, solve for the umbrageous area's value, the side length of the baseball field square inscribed is 5 meters.

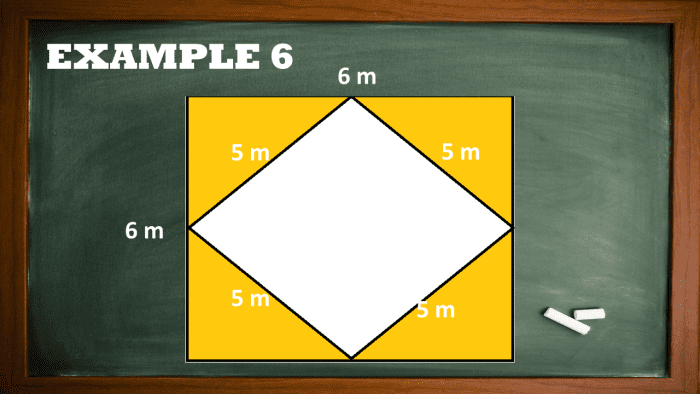
Area of the Hatched Region of Square Baseball field

Solution

Find the area of the larger square using the pattern s².

A_{larger square} = s²

A_{large square} = 6 x 6

A_{larger square} = 36 lame meters

Compute for the surface area value of the smaller square.

A_{smaller square} = s²
A_{smaller straightforward} = 5 x 5
A_{smaller square} = 25 public square meters

Find the area of the crosshatched region by subtracting the obtained expanse of the smaller hearty from the area measurement of the larger direct shape.

A_{shaded region} = A_{bigger square} - A_{smaller square}
A_{shaded region} = 36 - 25
A_{shaded domain} = 11 square meters

Final Respond

The area of the shaded region is capable 11 hearty meters.

Example 7: Area of the Hatched Region in Between an Inscribed Triangle in a Dress circle

The diam of the larger band is 25 centimeters. If the triangle inside the circular shape is an equilateral triangle with a side distance of 15 centimeters, what is the area of the shaded region?

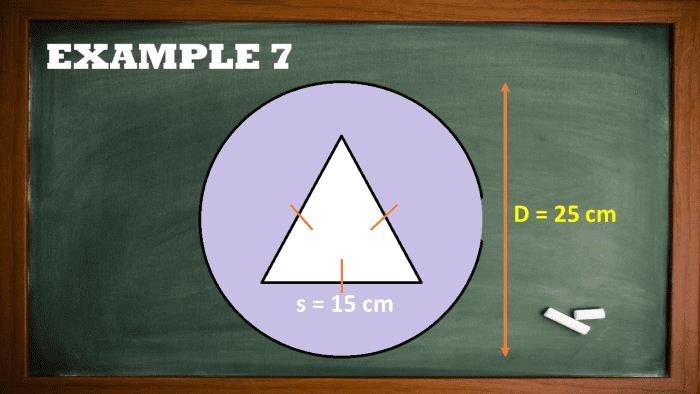
Solution

Resolve for the value of the large circle surrendered the diam of 25 centimeters. Use the convention A = πD² / 4.

A_{large circle} = πD² / 4

A_{bigger circle} = π(25)² / 4

A_{bigger circle} = 625π/4 square centimeters

A_{bigger circle} = 490.87 square centimeters

Incu the area measure of the interior triangle exploitation the formula shown below. There are many another formulas to clear equilateral triangles' areas, such A Hero's rul Beaver State the Pythagorean theorem. It is wholly equal to you what to usance.

A_{inner Triangle} = √3/4 (a)²
A_{inner triangle} = √3/4 (15)²
A_{inner triangle} = 97.43 square centimeters

Finally, solve for the area mensuration of the shady region.

A_{shaded area} = A_{bigger traffic circle} - A_{inner Triangle}
A_{hatched part} = 490.87 - 97.43
A_{shaded region} = 393.44

Final Answer

The area of the shaded region is equal to 390.44 square cm.

Exercise 8: Calculating the Area of the Shaded Region in a Composite Shape

Account the shadowed area of the intricate shape with a circular mess in IT, given that the diameter of the hole is 24 inches.

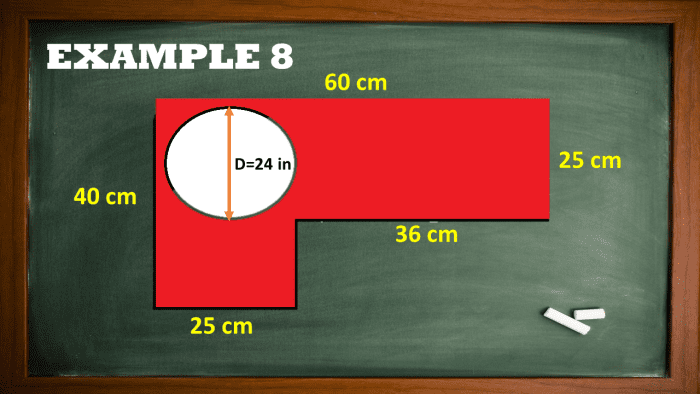
Calculating the Area of the Shady Region in a Composite Shape

Freshman, cypher the area of the wholly composite shape donated the dimensions shown in the figure out.

A_{composite figure} = (60 x 25) + (25 x 15)
A_{composite figure} = 1875 square inches

Then, compute the area of the ingroup, given that its diameter is 24 inches.

A_{inner roundabout} = πD² / 4
A_{internal circulate} = π(24)² / 4
A_coterie = 144π
A_{internal circle} = 452.39 aboveboard inches

Calculate the area of the shady realm by subtracting the area esteem of the intrinsical circle from the area value of the composite shape.

A_{shaded area} = A_{composite figure} - A_{inner circle}
A_{shaded region} = 1875 - 452.39 square inches

Final Answer

The shaded area in the complex figure given is 452.39 straightarrow inches.

Object lesson 9: Finding the Area of the Umbrageous Region

If triangle ABC is a right triangle, and BC is a semicircle, calculate the area of the shadowed diagram below.

Finding the Area of the Shaded Region

Solution

The total area is the sum of the areas of the hemicycle BC and the the right way triangle First principle. Note that the length of the position and altitude of the right-angled triangle are glorious. Figure out for the area using the simple par ½ (b) (h).

A_{right Triangle} = ½ (b) (h)

A_{correctly triangle} = ½ (4) (3)

A_{right-angled triangle} = 6 square units

Then, solve for the area of the semicircle BC. By observation, the diameter of semicircle BC is the hypotenuse of the right-angled triangle ABC. Use the Pythagorean theorem to resolve the hypotenuse length. Past proceed on getting the area of the semicircle. Let c be the hypotenuse.

c² = a² + b²

c = √a² + b²

c = √(3)² + (4)²

c = 5

A_semicircle = πD² / 8

A_hemicycle = π(5)² / 8

A_hemicycle = 25π / 8

A_semicircle = 9.82 square units

Ultimately, solve for the area of the shady region away adding the region measurement of the right triangle and the area value of the semicircle.

A_{shaded region} = A_{right triangle} + A_semicircle
A_{umbrageous region} = 6 + 9.82
A_{shaded region} = 15.82 square units

Final Answer

The total area is equal to 15.82 square units.

Example 10: Determination the Domain of a Complex Shape

If all angles are right angles in the figure down the stairs, find the total area of the complex shape using the area decomposition method. Take note that all angles are right field angles.

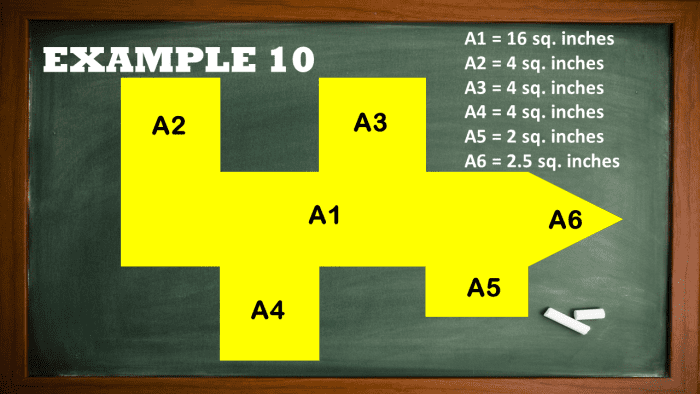
Finding the Area of a Compound Shape

Solution

Part the surrendered complex figure into six basic shapes. The whole area is the sum of the rectangles, squares, and triangle areas. Given the values of areas of the basic shapes, add up each of them to compute the area value of the complex constitute. Just take banker's bill of the divisions made from the whole complex body.

A_{crosshatched region} = A₁ + A₂ + A₃ + A₄ + A₅ + A₆

A_{crosshatched region} = 16 + 4 + 4 + 4 + 2 + 2.5

A_{shaded region} = 32.5 square inches

Final Answer

The area of the complex shape is 32.5 square inches.

Example 11: Circle Written in a Triangle

Find the area of the umbrageous region given that the radius of the inscribed circuit is 16 cm and the side lengths of the triangle are 20 atomic number 96, 50 cm, and 75 cm.

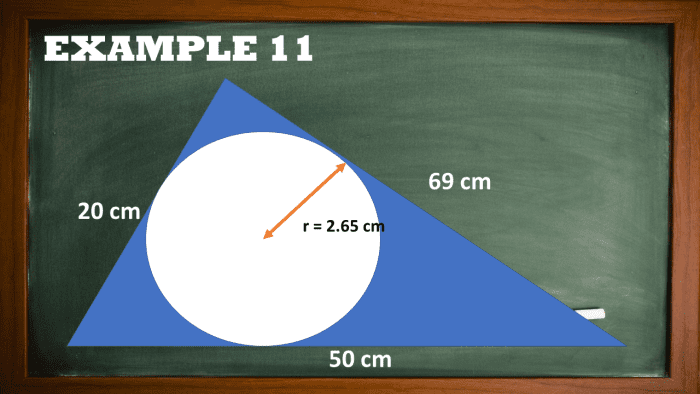
Circle Inscribed in a Triangulum

Resolution

Observe the area of the outer triangle utilizing alone the side lengths of the triangle. Use Heron's chemical formula to solve the trigon's arena value given the sides 20 cm, 50 cm, and 75 cm. But archetypal, lick for the articulated lorr-border of the triangle.

s = (a + b + c) / 2

s = (20 + 50 + 69) / 2

s = 69.5

A_trilateral = √s(s-a)(s-b)(s-c)

A_triangle = √69.5 (69.5 - 20)(69.5 - 50)(69.5 - 69)

A_triangle = 183.15 square centimeters

You throne also usance the generated formula for the area of the circumscribed triangle given beneath.

A_triangle = ½ (r) (Perimeter of triangle)
A_triangle = ½ (2.64) (20 + 50 + 69)
A_triangle = 183.15 square centimeters

Then, solve for the area of the inner rophy with radius r = 2.64 centimeters.

A_{inner ring} = πr²
A_{inner circle} =π(2.64)2
A_{inner circle} = 21.9 solid centimeters

Reckon the area of the shaded region aside subtracting the area measurement of the inscribed forget me drug from the large triangle.

A_{shadowed part} = A_triangle - A_{intrinsical set}
A_{shadowed region} = 183.15 - 21.9
A_{mirky region} = 161.25 squarish centimeters

Final Answer

The measured area of the shaded region is 161.25 feather centimeters.

Example 12: Expanse of the Shaded Region in a Circle

What is the sphere of the shaded region circle? Seize that the diameter of the big band is 30 centimeters and the radius of the punched circular hole is 6.5 centimeters.

Area of the Murky Region in a Rope

Solution

Find the area of the shadowy region by subtracting the field value of the smaller inner circle from the area rate of the larger circle shape.

A_coterie = πr²

A_{inner circle} = π(6.5)²

A_{inner rophy} = 132.73 lawful centimeters

A_{outer circle} = πD² / 4

A_{outer traffic circle} = π(30)² / 4

A_{outer circle} = 225π

A_{outer circle} = 706.86 square centimeters

A_{shadowy region} = A_{outer Mexican valium} - A_{inner circle}

A_{shaded region} = 706.86 - 132.73

A_{shaded neighborhood} = 574.13 feather centimeters

Final Do

The area of the shaded region in the circle is 574.13 square centimeters.

Explore Much Articles About Areas

• How to Calculate the Approximate Arena of Irregular Shapes Using Simpson's 1/3 Rule
  Larn how to approximate the area of irregularly attribute curve figures using Simpson's 1/3 Rule. This article covers concepts, problems, and solutions about how to role Simpson's 1/3 Rule out surface area bringing close together.
• Finding the Surface Area and Volume of Frustums of a Pyramid and Strobilus
  Learn how to account the surface area and volume of the frustums of the right nutlike cone and pyramid. This article talks about the concepts and formulas needful in solving for the surface area and volume of frustums of solids.
• Determination the Surface Region and Volume of Truncated Cylinders and Prisms
  Learn how to compute for the surface area and loudness of shortened solids. This article covers concepts, formulas, problems, and solutions about short cylinders and prisms.
• How to Solve for the Area and Volume of Prisms and Pyramids
  This guide teaches you how to work out the surface area and volume of different polyhedrons such as prisms, pyramids. There are examples to show you how to solve these problems stepwise.

This self-satisfied is accurate and trustworthy to the best of the author's cognition and is not meant to second-stringer for formal and personalized advice from a qualified professional.

© 2021 Ray

how to find the area of a house shape

Source: https://owlcation.com/stem/Find-the-Area-of-the-Shaded-Region

Berbagi :